Расчет числа витков катушек индуктивности
Главная / ЭКВМ / Программы для ЭКВМ / Расчёты в технике

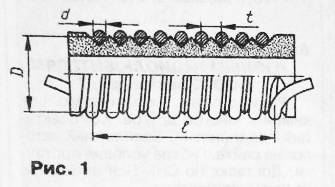
Автор программы: В. Миронов, дер. Гостилицы Ленинградской обл.

Опубликована: журнал "Радио" N3, 2007 г. (редактор - Л. Ломакин, графика - Л. Ломакин).

Описание

В некоторых справочниках можно найти формулу для расчёта индуктивности однослойной катушки:

L = n(A·n + B/n - C), где:

A = (πD)2/l + 0,45D

B = 3,5l·D/d;

C = 4D.

Эта формула пригодна для расчёта индуктивности катушки, если известны её параметры (рис. 1): D - диаметр катушки; d - диаметр провода; l - осевая длина катушки; n - число витков.

Параметры однослойной катушки индуктивности

Но иногда необходимо намотать однослойную катушку определённой индуктивности на готовый каркас с канавками для укладки провода с шагом t и, значит, определить требуемое число витков. Если поперечное сечение не круг, а правильный многоугольник, то в указанных выше соотношениях диаметр D заменяют на D0cos2(π/2N), где D0 - расстояние между соседними вершинами многоугольника плюс диаметр провода; N - число граней многоугольника.

Задача сводится к решению нелинейного уравнения L - n(A·n + B/n - C) = 0 относительно n. Такая методика особенно удобна для расчёта числа витков однослойной катушки, намотанной виток к витку, - t=d, а длина катушки l=d·n.

Для решения предназначена простая программа для калькулятора. Думаю, она будет интересна тем радиолюбителям, у которых ещё сохранились программируемые калькуляторы "Электроника МК-61" или другие.

Программа katushki1.mkp (КС 11647/175)

  0 1 2 3 4 5 6 7 8 9
00 П 7 ИП 4 4 × П C 0 П 2 1 0 П 3
10 ИП 2 ИП 3 + П 2 ИП 8 × П 5 3 , 5
20 × ИП 4 × ИП 6 ÷ П B F π ИП 4 × F x2
30 0 , 4 5 ИП 4 × ИП 5 + ÷ П A
40 ИП 2 × ИП B ИП 2 ÷ + ИП C - ИП 2 /-/
50 × ИП 7 + F x<0 10 ИП 2 ИП 3 - П 2 С/П
60 ИП 3 1 0 ÷ П 3 БП 10      

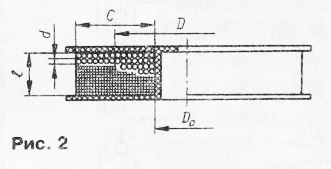
Примечание. В журнале текст программы напечатан с ошибкой: первая команда должна иметь нулевой адрес.

Ввод: D = P4; d = P6; t = P8; L = PX.

Вывод: n = PX = P2; l = P5.

Пример: D = 2 см = P4; d = 0,1 см = P6; t = 0,15 см = P8; L = 2000 нГн = PX.

Нажимаем на [В/О],[С/П], ждём, нажимаем на [С/П], ждём, ещё раз нажимаем на [С/П], ждём, повторно нажимаем на [С/П], ждём и получаем n=PX=P2 = 11,4 витка (округлённо, или 11,42 точно). (11,42). l=P5 = 1,7 см (округлённо, или 1,7145 см точно).

Каждое очередное нажатие на клавишу [С/П] даёт следующий десятичный знак.

Иногда бывает необходимо рассчитать число витков короткой многослойной катушки. В [1] и [2] описан расчёт катушки, исходя из её геометрических размеров. По полученным результатам можно вычислить требуемый диаметр провода, которого у радиолюбителя может и не быть. Я хочу предложить программу расчёта, в котором исходным параметром служит диаметр провода. Она была использована при проектировании LC-фильтров для акустической системы.

Исходные параметры (рис. 2): l - осевая длина катушки; D0 - внутренний диаметр; d - диаметр провода; L - индуктивность катушки. Результатом расчёта будут n - число витков и C - высота обмотки. Короткой принято называть многослойную катушку, у которой длина меньше среднего диаметра обмотки: L<D.

Параметры многослойной катушки индуктивности

Формула для расчёта числа витков из [1] была видоизменена:

L - 25π·n2(C+D0)2 / [2 (C+D0)+ 9l + 10C] = 0,

где C = n·d2Kу/l.

Если витки обмотки уложены неплотно (например, внавал), необходим коэффициент, учитывающий эту неплотность. Коэффициент укладки Kу показывает, во сколько раз реальная площадь C·l, занятая обмоткой, больше идеальной, когда витки уложены плотно один к другому в абсолютно ровные ряды.

Определить Kу можно опытным путём, намотав на каркас, подобный рассчитываемому, пробную обмотку.

Зная число витков пробной обмотки nпроб, вычисляют площадь сечения идеальной обмотки по формуле

Sид = nпроб·d2.

Измеряют площадь пробной обмотки

Sпроб = Cпроб·lпроб

и вычисляют Kу = Sпроб/Sид.

Этот коэффициент может принимать значения, большие единицы или равные ей.

Программа для "Электроники МК-61" выглядит следующим образом:

Программа katushki2.mkp (КС 12638/178)

  0 1 2 3 4 5 6 7 8 9
00 П 9 0 П 2 1 0 0 П 3 ИП 2 ИП 3 +
10 П 2 ИП 6 F x2 × ИП 5 × ИП 8 ÷ П C ИП 7
20 + П 1 F x2 F π × 2 5 × ИП 2 F x2
30 × ИП 1 3 × ИП 8 9 × + ИП C 1
40 0 × + ÷ /-/ ИП 9 + F x<0 07 ИП 2
50 ИП 3 - П 2 С/П ИП 3 1 0 ÷ П 3 БП
60 07                  

Примечание. В журнале текст программы напечатан с ошибкой: первая команда должна иметь нулевой адрес.

Ввод: Kу = P5; d = P6; D0 = P7; l = P8; L = PX.

Вывод: n = PX = P2; C = PC.

Контрольный пример: Kу = 1,3 = P5; d = 0,055 см = P6; D0 = 0,8 см = P7; l = 0,8 см = P8; L = 200 000 нГн = PX.

Нажимаем на кнопки [В/О], [С/П], [С/П], [С/П], [С/П] с перерывами на время счёта и получаем n = 144,9 = PX = P2; C = PC = 0,713 см (0,71276562 точно). Каждое нажатие на кнопку [С/П] даёт следующий десятичный знак.

Если получилось l > (C + D0), следует использовать провод большего диаметра или каркас с меньшим значением l и пересчитать n.


Литература

1. Дьяконов В.П. Справочник по расчётам на микрокалькуляторах. Изд 2-е - М.: Наука, 1986.

2. Дьяконов В.П. Справочник по расчётам на микрокалькуляторах. Изд 3-е. - М.: Наука, 1989.


Текст статьи незначительно изменён, оригинал:

Расчет числа витков катушек индуктивности
НПП "СЕМИКО" (383) 271-01-25 (многоканальный)