Решение квадратного уравнения на ЭКВМ

  Программа для решения квадратного уравнения на программируемых калькуляторах так же традиционна, как вывод "Hello, World" в учебниках по Си. И это неспроста. Нахождение корней алгебраических уравнений - типичная задача обработки числовых данных, не требующая больших вычислительных ресурсов.

Вспомним математику. Корни x₁ и x₂ квадратного уравнения: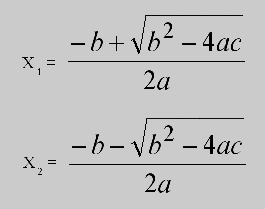

ax² + bx + c =0 определяются по формулам:

Напишем программу для ЭКВМ "Электроника МК", которая решает это уравнение. Такую простую программу можно набрать прямо из головы, глядя только на формулы.

Положим RA=a, RB=b, RC=c. Это означает, что перед запуском программы в перечисленные регистры следует занести нужные коэффициенты. Регистр RD используем для хранения дискриминанта:

D=b²-4ac.

Квадратное уравнение 1

Программа занимает 28 байт. Здесь и в других аналогичных случаях для перемещаемых программ небольшого размера приведены адреса в пределах одной страницы, т.е. 100 шагов. В ЭКВМ программы старых калькуляторов могут быть загружены в любую страницу памяти, но будем предполагать, что программа записана в нулевую страницу - с адреса 0000. Это позволит переходить на начало программы нажатием клавиши "В/О".

В адресах 00-08 вычисляется дискриминант. В 09-17 находится первый корень, в 18-26 - второй. После останова по адресу 27 в регистрах стека X и Y будут корни уравнения. Если уравнение не имеет действительных корней, то после попытки нахождения квадратного корня из отрицательного числа по адресу 12 возникнет ошибка и будет выведено сообщение "ERROR". Для повторения расчёта следует занести в память новые коэффициенты и нажать клавиши "В/О", "С/П".

Для решения школьных задач эта программа вполне пригодна. Она одинаково выполняется как на старых калькуляторах, так и ЭКВМ. Хотя результат расчёта по одной и той же программе на них может отличаться вследствие различной погрешности при вычислениях.

После незначительных и очевидных сокращений можно получить следующую программу длиной 24 байта. Имея некоторый опыт её также несложно составить в уме и ввести в ЭКВМ без предварительной записи на бумаге.

Квадратное уравнение 2

При этом не следует рассматривать сокращение размера программы как особую цель. Глубокая оптимизация программ в калькуляторах была зачастую вынужденной мерой, в ЭКВМ же ресурсов куда больше. Программа, если она разрабатывается для решения конкретной задачи, должна быть оптимальна не только по размеру и быстродействию, но и по трудозатратам.

Значительную оптимизацию можно получить правильным выбором алгоритма. Для решения уравнений на калькуляторах существуют различные алгоритмы, позволяющие сократить объём программы или уменьшить погрешность расчётов.

Введём дополнительную переменную r = -b/a и запишем формулы корней уравнения в следующем виде:

x₁ = r + √(r²-c/a),
x₂ = r - √(r²-c/a).

Если значение подкоренного выражения меньше нуля, то x₁ и x₂ - комплексно сопряжённые корни. Для школьной математики это означает, что уравнение "не решается". В приведённых ниже программах вычисляется действительная часть корней r и отдельно коэффициент при мнимой части.

Рассмотрим следующую программу, которая выполняет расчёт по этим формулам. Откроем "Справочник по расчетам на микрокалькуляторах", автор В.П. Дьяконов [1], и найдём программу вычисления корней квадратного уравнения. Она приведена ниже с небольшими изменениями для сохранения удобочитаемости. В оригинале коэффициенты уравнения имеют обозначения a₂, a₁ и a₀, а для их хранения используются регистры R2, R1 и R0 соответственно.

Квадратное уравнение 3

Для вычисления корней следует ввести в RA, RB, RC коэффициенты. Нажать клавиши "В/О" и "С/П". Вывод результатов: на индикаторе число 7, если корни действительные и 4, если комплексно сопряженные. Действительные корни выводятся в регистры Y и R7. Комплексные - вещественная часть в Y, мнимая в R4. При вводе нуля в RA, то есть в случае попытки решения линейного уравнения, будет выведено сообщение об ошибке "ERROR".

Это типичная программа для ПМК. Она подходит для вычисления корней квадратных уравнений в большинстве случаев. Вся программа занимает 28 байт. Команды по адресам 00-06 вычисляют значение r. Команды 07-11 вычисляют подкоренное выражение. Сравнение с нулём в 12-13 позволяет перейти на адрес 18, если корни вещественные. Далее в 14-15 производится вычисление вещественной части корней, если они комплексно сопряжённые. По адресам 16 и 17 расположен останов с индикацией числа "4". В 18-28, после перехода с адреса 12 вычисляются вещественные корни. В 18-22 вычисляется первый корень, в 23-25 второй. По адресам 27-28 расположен останов с индикацией числа "7".

Без каких-либо изменений эта программа может использоваться на ЭКВМ. Она проста, компактна и достаточно удобна в использовании.

Выбор подходящего алгоритма может приводить и к значительному снижению погрешности вычислений. В случае квадратного уравнения, меньший по модулю действительный корень может быть определён при помощи выражения:

x₂ = -c/(a*x₁),

где x₁ - больший по модулю корень.

Соответствующая программа также есть в упомянутом справочнике [1]. Она приведена без изменений.

Квадратное уравнение 4

Коэффициенты уравнения заносятся в регистры RA, RB и RC перед запуском программы. После останова на индикатор в регистр X выводится число 7, если корни действительные, или 4, если комплексно сопряжённые. В первом случае значения корней x₁ и x₂ следует считывать из регистров R7 и R8. Во втором - действительная часть находится в R4, мнимая в R5. При этом x_1,2 = R4 +- j R5, где j = √-1.

Командами по адресам 00-04 вычисляется коффициент -с/а и заносится в R9. В 05-10 вычисляется значение r и помещается в R4. В адресах 11-14 находится подкоренное выражение из формул, взятое с обратным знаком и сравнивается с нулём. Если оно положительно, то корни комплексные. В этом случае происходит переход на адрес 31, вычисление и занесение мнимой части в регистр R5, после чего останов с выводом на индикатор числа 4. Если переход с адреса 13 не происходит - корни действительные. В 15-16 по вычисляется значение квадратного корня. Далее в 17-19 проверяется величина r. Если она больше нуля, то x₁>x₂ и наоборот. В зависимости от этого сложением или вычитанием в 20-24 находится наибольшее по модулю значение и записывается в R7. Здесь использован интересный приём - сложение с нулем вместо ветвления для обхода команды "+" по адресу 23. Команда "↔" выполняет обмен содержимого регистров стека X и Y. В адресах 25-28 находится второй корень и записывается в R8. В 29-30 происходит останов с выводом числа 7 на индикатор.

Нетрудно заметить, что эта программа несколько длиннее предыдущих и не столь понятна с первого взгляда. Зато она в некоторых случаях дает заметное преимущество в точности вычислений. В таблице приведены результаты работы программ при вычислении корней некоторых уравнений. Тестовые примеры взяты из справочника [1]. Следует заметить, что точные значения корней и погрешности ПМК указаны в нем с ошибкой.

На индикатор МК-152 и МК-161 (в обычном режиме) числа будут выведены с округлением до восьми знаков.

Примером использования алгоритма решения квадратного уравнения для изучения системы команд ПМК является следующая программа, взятая из руководства по эксплуатации калькулятора МК-61 [2]. Она предназначена для демонстрации действия команды косвенного обращения к подпрограмме.

Квадратное уравнение 5

Команды 00-02 заносят в R7 адрес начала подпрограммы. Команда КПП7 по адресу 03 вызывает обращение к подпрограмме, расположенной по адресу, который записан в R7, в данном случае 19. Подпрограмма 19-31 вычисляет по дискриминант и величину -b и записывает их в регистры Y и X стека. Команда "В/О" по адресу 31 вызывает возврат из подпрограммы. Возврат происходит на адрес, следующий за командой вызова подпрограммы, в данном случае 04. Команды 04-09 вычисляют значение первого корня и заносят его в R1. Команда КПП7 по адресу 10 повторно вызывает подпрограмму 19-31. Возврат из неё произойдёт к команде по адресу 11. В 11-17 вычисляется значение второго корня, которое помещается в R2. Команда "С/П" по адресу 18 завершает выполнение программы.

Пример этот, быть может, не вполне удачен. Повторное вычисление дискриминанта замедляет вычисления. Да и само косвенное обращение вместо прямого занимает лишний шаг. Лучше было бы показывать действие команд в тех местах, где они необходимы. Но сама программа вполне работоспособна, а применённые в ней приёмы могут быть полезны в других случаях.

Следующая программа является вариантом предыдущей и тоже использует подпрограмму, но обращается к ней напрямую. Экономия нескольких команд достигается также более корректным использованием стека.

Квадратное уравнение 6

Команда "ПП 16" по адресам 00-01 и 09-10 вызывает обращение к подпрограмме 16-27. Команда "В↑" по адресу 18 поднимает стек и копирует -b в регистр Y. Для операции возведения в квадрат по адресу 19 знак аргумента значения не имеет. В остальном программа аналогична предыдущей.

Рассмотрим более сложный вариант. Если a равно нулю, то уравнение из квадратного превратится в линейное и приведённые выше формулы будут некорректны. Для этого случая требуется отдельное решение:

x₀=-c/b.

Если в этом случае b=0 и c≠0, то решения нет. Если b=0 и c=0, то x0 - любое число, поскольку уравнение примет вид тождества 0=0.

В таком варианте задача подробно рассмотрена в книге "Секреты программируемого калькулятора", автор И.Д.Данилов [3]. Приводимая далее программа взята из этой книги.

Квадратное уравнение 7

Для использования программы в регистр R0 помещается код окончания "Корней нет", в R3 - "Один корень", в R4-"Два действительных корня", в R5 - "Корни комплексные". Для формирования сообщений в книге [данилов] использовались недокументированные возможности ПМК, точнее некорректная работа оператора "ВП", позволявшая после ряда действий получить "числа" наподобие "Г.", "Е00", "Е01" и т.п. В ЭВМ этот оператор работает корректно, поэтому в регистры следует занести произвольные числовые коды, например "0", "1", "2" и "3".

Перед пуском программы следует ввести коэффициент a, после первого останова - b, после второго - с. Последовательность запуска программы выглядит таким образом: "В/О", ввод a, "С/П" ввод b, "С/П", ввод c, "С/П". После первого останова на индикатор выводится числовой код окончания. Если корней нет, то можно повторить ввод коэффициентов и запустить программу повторно. Если корни есть, то нажать "С/П". После останова в регистре X - первый корень или мнимая часть комплексных корней. В регистре Y - второй корень, если он есть, или действительная часть комплексных корней.

Разбирать, как работает эта программа, наверное, незачем. Подробный анализ алгоритма есть в книге [3], из которой она взята.

Команда "F ↻" ("F O")в адресах 06, 44 и 57 выполняет поворот стека. При этом содержимое регистра X записывается в T, T в Z, Z в Y, а Y в X. Команда "F Bx" в 53 вызывает в регистр X из регистра X1 результат предыдущей операции. В данном случае результат сложения по адресу 51.

Нетрудно заметить, что программа написана не вполне оптимально. Это сделано намеренно, чтобы продемонстрировать работу всех ветвей алгоритма. Далее приведена блок-схема, на которой дополнительно указаны адреса команд, соответствующих элементам схемы.

В [3] есть более компактный вариант программы. В ней изменён порядок вывода результатов. После останова и вывода в регистр X кода не следует нажимать клавишу С/П для вывода значений корней. После первого останова они находятся в регистрах стека Y и Z.

В ПМК корни можно командой "F O" поочерёдно считать из регистра X, отображаемого на индикаторе. В ЭВМ все регистры стека выводятся одновременно. Поэтому дополнительных команд для считывания полученных значений не требуется.

Квадратное уравнение 8

В исходной программе из [3] большое количество безусловных переходов. В этой версии они заменены на команду "В/О". Эта команда программы, если она используется вне подпрограммы, передаёт управление на адрес 01. Иначе говоря, заменяет двухбайтовую команду "БП 01". Эта особенность ПМК воспроизведена и в ЭВМ. По адресу 00, с которого начинается выполнение программы в первый раз после запуска, находится команда "КНОП", которая никаких действий не выполняет.

Как и предыдущие программы решения квадратного уравнения, эта будет одинаково выполняться как на ПМК (Б3-34, МК-52, МК-61 и т.п.), так и на клавишных ЭВМ "Электроника МК-152" и "Электроника МК-161".

Литература

1. Дьяконов В.П. Справочник по расчетам на микрокалькуляторах. - 2-е изд, испр. - М.: Наука. Гл. ред. физ.-мат. лит., 1986. - 224 с.
2. Микрокалькулятор "Электроника МК-61". Руководство по эксплуатации. - ППО "Укрвузполиграф" - 1987.
3. Данилов И.Д. Секреты программируемого микрокалькулятора. - М.: Наука. Гл. ред. физ.-мат. лит., 1986. - 160 с. - (Б-чка "Квант". Вып. 55.)