График параметрически заданной функции

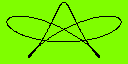
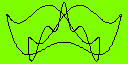
График параметрически заданной функции определяется системой уравнений x=x(t); y=y(t), где t - параметр.

Приведённая программа в качестве примера строит фигуры, являющиеся расширением фигур Лиссажу. Фигуры Лиссажу являются траекторией точки, совершающей гармонические колебания одновременно в двух взаимно перпендикулярных направлениях. То есть фигура Лиссажу описывается системой уравнений: x=a*cos(bt+c); y=d*cos(et+f), где a,b,c,d,e,f - константы, t - параметр.

Классические фигуры Лиссажу представляют собой замкнутые траектории, при равенстве периодов (константы b и e в уравнениях выше) - эллипсы. Которые вырождаются в отрезки прямых при разности фаз (константы c и f) равной 0 или кратной π или в окружность при равенстве амплитуд (a и d) и разности фаз кратной π/2. Фигуры Лиссажу вписаны в прямоугольник, стороны которого параллельны осям координат, а размеры определяются амплитудой колебаний.

Если колебания по каждой координате определить как сумму гармонических колебаний с различными амплитудами, периодами и фазами - получим параметрически заданные функции, являющиеся более сложными объектами, чем простые фигуры Лиссажу.

В приведённой программе используются функции вида: x=R8*sin(R7*t) + RA*cos(R9*t); y=RC*sin(RB*t) + RE*cos(RD*t). Чтобы не мудрить с дальнейшим переобозначением, константы в этих уравнениях указывают на регистр памяти ЭКВМ.

Нетрудно заметить, что начальная фаза в этих уравнениях не задаётся. Фиксированный сдвиг по фазе на π/2 между колебаниями по одной координате обеспечивается использованием различных тригонометрических функций.

Перед запуском программы следует занести дополнительные параметры: шаг по t в R3, верхний диапазон значений t в R6. Значение в R3 определяет качество и скорость рисования графика, которые находятся между собой в обратной зависимости. Значение в R6 должно обеспечивать замкнутость траектории.

Теоретически, при строго иррациональном соотношении периодов, кривая никогда не замкнется, в пределе заполнив всю область прямоугольника. На практике, рациональность чисел обеспечивается ограничением числа разрядов в ЭКВМ, также следует учитывать ограниченную разрешающую способность индикатора и скорость вывода.

Для вывода классических фигур Лиссажу следует задать нулевые параметры амплитуды в RA и RC. Для наблюдения влияния сдвига фаз - переписать подпрограммы вычисления x(t) и y(t).

Приведённые графики сняты при заданных значениях: 0,01 П3 (шаг по t); Fπ 2 x П6 (2π - диапазон t). Амплитуды колебаний: 40 П8; 20 ПА ПС; 10 ПЕ. Изменялись только соотношения периодов, указанные отдельно.
	x=4sin(t)+2cos(2t); y=2sin(2t)+cos(t) 1 П7; 2 П9 ПВ; 1 ПД
	x=4sin(t)+2cos(3t); y=2sin(2t)+cos(t) 1 П7 ПД; 3 П9; 2 ПВ
	x=4sin(t)+2cos(3t); y=2sin(3t)+cos(t) 1 П7 ПД; 3 П9 ПВ
	x=4sin(2t)+2cos(3t); y=2sin(3t)+cos(t) 2 П7; 3 П9 ПВ; 1 ПД
	x=4sin(2t)+2cos(3t); y=2sin(3t)+cos(2t) 2 П7 ПД; 3 П9 ПВ
	x=4sin(2t)+2cos(3t); y=2sin(3t)+cos(3t) 2 П7; 3 П9 ПВ ПД
	x=4sin(2t)+2cos(3t); y=2sin(3t)+cos(4t) 2 П7; 3 П9 ПВ; 4 ПД
	x=4sin(2t)+2cos(3t); y=2sin(3t)+cos(10t) 2 П7; 3 П9 ПВ; 10 ПД
	x=4sin(7t)+2cos(3t); y=2sin(3t)+cos(10t) 7 П7; 3 П9 ПВ; 10 ПД
	x=4sin(4t)+2cos(5t); y=2sin(3t)+cos(10t) 4 П7; 5 П9; 3 ПВ; 10 ПД
	x=4sin(2t)+2cos(5t); y=2sin(3t)+cos(2t) 2 П7 ПД; 5 П9; 3 ПВ

Программа

Часть программы, отвечающая за вывод графика, занимает 45 байт. Общая длина программы, вместе с уравнениями - 73 байта.

Контрольная сумма ADD 11975, контрольная сумма XOR 143 - при условии что остальные байты содержат 0FFh.

Структура программы

00-09 - инициализация;

10-11 - определение координат начальной точки;

12-23 - приращение t, проверка окончания и останов;

24-31 - обращение к подпрограмме 32 и отрисовка линии;

32-44 - подпрограмма вычисления координат точки;

45-58 - подпрограмма вычисления x(t);

59-72 - подпрограмма вычисления y(t).

Исходный текст для компилятора

; Программа "Фигуры Лиссажу"
; Построение графика параметрически заданной функкции
; Версия 1.1
; R0=T
; R1=X
; R3 - приращение по T
; R6 - ограничение по T 
; R7-RE - коэффициенты
; X=R8*sin(R7*t) + RA*cos(R9*t)
; Y=RC*sin(RB*t) + RE*cos(RD*t)

.CHARSET 1251
.ORG 0

	;Инициализация
	CX M0

	; Сброс графики
	2 PP M 9010

	1 PP M 9045	; установить размерность - радианы

	; Найти начальную точку
	GSB PT
A0:	PP M 9000	; Переместить координаты
	RM0 RM3 + M0
	RM6 -
	F X>=0 A1
	R/S
A1:	GSB PT
	PP M 9012	; Линия
	K GRPH
	GOTO A0;

PT:	GSB FX
	64 + M1
	GSB FY
	32 +
	RM1
	RTN

FX:	;R8*sin(R7*t) + RA*cos(R9*t)
	RM0 RM7	* F SIN	RM8 *
	RM0 RM9 * F COS	RMA *
	+
	RTN

FY:	;RC*sin(RB*t) + RE*cos(RD*t)
	RM0 RMB * F SIN RMC *
	RM0 RMD * F COS RME *
	+
	RTN
.END

Файлы программ и данных:

lissa1.mkl - текст программы для компилятора (755 б);

lissa1.mkp - программа на языке ЭКВМ (201 б);