Решение дифференциального уравнения методом Рунге-Кутта

Условия

Условия задачи были поставлены здесь:
http://shura.luberetsky.ru/2009/04/28/reshaem-uravnenie-burbulyatora/

Решение уравнения бурбулятора методом Рунге-Кутта

Предлагаю сравнить несколько языков программирования (в широком смысле) по критерию их удобства для разнообразных расчетов. Даю вводную: из коробки извлекается компьютер (или вообще какое-нибудь вычислительное устройство, желательно с экраном), и необходимо в кратчайший срок произвести на нем сравнительно несложные вычисления.

Чтобы не извращаться, возьмем возникающее из физики уравнение Ван-дер-Поля. Речь идет о “модификации” уравнения осциллятора

y” + ay’ + y = 0.

Как легко показать (ну-ка, кто умеет решать дифференциальные уравнения?) при a>0 колебания будут затухающими, а при a<0 - неустойчивыми, то есть система пойдет вразнос. При a=0 получится малоинтересное уравнение идеального колебательного контура, которого в природе не бывает. Параметр a играет здесь роль сопротивления.

Теперь подставим вместо константы a изменяющуюся величину (например, включив в цепь триод). В качестве простого "идеализированного" триода выберем a = y2 - 1. Тогда уравнение превратится в

y” + (y2-1)y’ + y = 0,

или, после стандартного понижения порядка - в систему двух уравнений:

y’1=y2

y’2=(1 - y12)y2 - y1

Как показал в 1920-1926 году Ван-дер-Поль, у такой системы сущеcтвует устойчивое периодическое решение, к которому сходятся все остальные решения. Это не может не радовать, так как система возникла из математического описания генератора незатухающих колебаний на триоде (кстати, для 20-х - вполне себе чудо техники).

Необходимые же вычисления заключаются в том, чтобы численно промоделировать это уравнение. Предлагаю воспользоваться методом Рунге-Кутта в его простейшей форме. Пусть у нас есть система дифференциальных уравнений

y’1=f1(x, y1, y2)

y’2=f2(x, y1, y2),

мы умеем вычислять функции f1 и f2 в любой точке, и нам известны значения y1, y2 в точке x0. Тогда мы можем приближенно вычислить их значения в точке x1 = x0 + h, где h достаточно мало, по следующим формулам (в “Кратком физико-математическом справочнике” Аленицына, Бутикова и Кондратьева 1990 года издания они приведены, как “формулы Рунге-Кутта”):

p11 = hf1(x0, y1, y2)

p12 = hf2(x0, y1, y2)

p21 = hf1(x0 + h/2, y1 + p11/2, y2 + p12/2)

p22 = hf2(x0 + h/2, y1 + p11/2, y2 + p12/2)

p31 = hf1(x0 + h/2, y1 + p21/2, y2 + p22/2)

p32 = hf2(x0 + h/2, y1 + p21/2, y2 + p22/2)

p41 = hf1(x0 + h, y1 + p31, y2 + p32)

p42 = hf2(x0 + h, y1 + p31, y2 + p32)

x1 = x0 + h

y1(x1) = y01 + (p11 + 2 p21 + 2 p31 + p41) / 6

y2(x1) = y02 + (p12 + 2 p22 + 2 p32 + p42) / 6

Конечно, в современной вычислительной практике применяются гораздо более сложные варианты метода Рунге-Кутта, например, формулы Дормана-Принса, но для грубых расчетов хватит и этого. Не будем усложнять задачу такими “бонусами”, как автоматический выбор длины шага, а ограничимся этими формулами. Для упрощения написания программы я “раскрыл” вектор (y1, y2). Для вычисления y1(x1) и y2(x1) достаточно лишь применить эти формулы в том порядке, в котором они выписаны. Вычисления надо повторять, пока не исчерпается отрезок, на котором нас интересуют значения y(x).

Теперь для расчетов требуются лишь начальные условия - известные в нулевой момент времени y1 и y2, а также величина шага и длина отрезка интегрирования. Предлагаю выбрать такие начальные условия:

x0 = 0,

y1(0) = 0,

y2(0) = 0,0001

Очень небольшое значение y2 - необходимый для запуска генератора “толчок”. Я утверждаю, что при таких условиях y1(x) довольно быстро “стабилизируется” и колебания станут незатухающими, с постоянной частотой. Для того, чтобы убедиться в этом, предлагаю проделать вычисления с шагом 0,1 вплоть до x = 64. Получим довольно симпатичный график (масштаб по y - в десять раз меньше, чем по x):

Предлагаю всем желающим попробовать построить такой же график любыми доступными с компьютером “из коробки” средствами. К таковым, например, можно причислить Excel - офисный пакет довольно часто является предустановленным, Matlab же к “коробочным” не относится. Разнообразные варианты Basic - от Sinclair Basic до VBScript, Javascript, различные варианты интерпретатора командной строки - только приветствуются. Интересно было бы взглянуть на программу для какого-нибудь программируемого калькулятора (при отсутствии графического экрана достаточно просто “распечатки” значений). Сомневаюсь, что “старинные” МК-52 или МК-61 “потянут” это, памяти у них маловато (хотя метод Ньютона для них реализовывали), а вот для МК-152 такая задача - в самый раз.

PS Я свой график строил на QBasic из комплекта MS-DOS 6.22

Решение на ЭКВМ

Программа на языке ЭКВМ

Для решения задачи на ЭКВМ Электроника МК-152 или МК-161 была составлена программа длиной 246 байт:

Контрольная сумма ADD 30997, контрольная сумма XOR 25 - при условии что остальные байты содержат 0FFh.

Результат работы программы

После запуска программы на экран по точкам выводится искомое решение.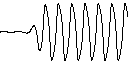

Если преобразовать накопленные в блокноте значения при помощи электронной таблицы, можно постоить более точный график. Для обработки содержимого блокнота использована программа OpenOffice.org Calc.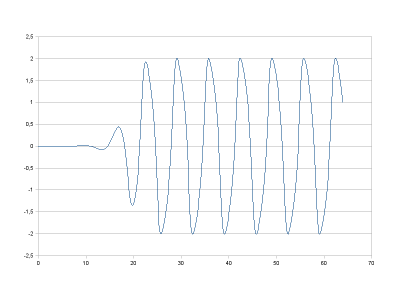

После запуска обнаружена и в версии 1.1 исправлена ошибка, связанная с направлением оси Y при выводе графика. Расчётные значения точек в блокноте - без изменения.

Время работы при выводе графика в процессе работы программы 2 мин. 10 сек.

Время работы при с выводом графика после окончания работы программы 1 мин. 25 сек. Для этого по адресу 98 заменить команду "К ГРФ" на "К НОП". Команду "К ГРФ" выполнить после окончания работы программы.

Одновременно с этим накапливаются данные в электронном блокноте ЭКВМ. Часть данных здесь пропущена.

Блокнот МК

Исходный текст для компилятора

; Программа "Уравнение бурбулятора"
; Версия 1.1 - исправлено направление оси Y при выводе, более корректная проверка конца экрана
; Численное моделирование решения дифференциального уравнения Ван-дер-Поля методом Рунге-Кутта
; http://shura.luberetsky.ru/2009/04/28/reshaem-uravnenie-burbulyatora/
; R0=X
; R1, R2 = y1,y2 для F1,F2
; RB, RC = y1(i), y2(i)
; RE=h
; R3-11,R4-12,R5-22,R6-23,R7-31,R8-32,R9-41,RA-42

; R20- счётчик блокнота
; R21 - координата X экрана

.CHARSET 1251
.ORG 0
	;Инициализация
	CX
	PM 20
	PM 21
	MB
	
	1 EE 4 +/- MC
	0,1 ME

	;Сброс графики
	2 PP M 9010
	32 ENT CX PP M 9000

A1:	;Запомнить старые X,Y1,Y2
	PRM 20
	PP M 9060	; группа записи блокнота
	1 + 
	PM 20 
	RM0 	PP M 9061	;X
	RMB 	PP M 9062	;Y1
	RMC	PP M 9063	;Y2
	CX	PP M 9064

	;Точка на экране
	PRM 21
	128
	-
	F X<0 A11
	GOTO A2
A11:	2
	PP M 9010	; Сброс экрана
	CX
	PM 21
	RMB
	P GSB PIX
	CX
	PP M 9000

	GOTO A3
A2:	PRM 21
	0,2
	+
	PM 21

A3:	RMB
	P GSB PIX
	PRM 21
	PP M 9012
	PP M 9000
	K GRPH

	; Следующая точка
	;P11
	RMB M1
	RMC M2
	P GSB	F1
	RME * M3

	;P12
	P GSB	F2
	RME * M4
	
	;P21
	RM3 2 / RMB + M1
	RM4 2 / RMC + M2
	P GSB	F1
	RME * M5

	;P22
	P GSB	F2
	RME * M6

	;P31
	RM5 2 / RMB + M1
	RM6 2 / RMC + M2
	P GSB	F1
	RME * M7

	;P32
	P GSB	F2
	RME * M8

	;P41
	RM7 RMB + M1 
	RM8 RMC + M2
	P GSB	F1
	RME * M9

	;P42
	P GSB	F2
	RME * MA

	; Новые X,Y1,Y2
	;X
	RM0 RME + M0
	
	;Y1
	RM3 RM5 2 * + RM7 2 * + RM9 + 6 / RMB +	MB

	;Y2
	RM4 RM6 2 * + RM8 2 * + RMA + 6 / RMC + MC

	;Проверка и цикл 
	RM0 64	-
	P X>=0 A1 
	R/S

F1: 	;y'1=y2 
	RM2
	RTN

F2:	;y'2=(1-y1^2)*y2-y1
	1 RM1 F X^2 - RM2 * RM1	-	
	RTN

PIX:	14 * +/- 32 +
	RTN
.END

Файлы программ и данных:

burbuljator1.mkl - текст программы для компилятора (1,7 кб);

burbuljator1.mkp - программа на языке ЭКВМ (601 б);

burbuljator1.mkn - блокнот ЭКВМ, записи от 0 до 639 (20,0 кб);

burbuljator1_mkn.txt - содержимое блокнота в текстовом виде, поля разделены табуляцией (33,0 кб).

burbuljator1.ods - файл электронной таблицы OpenOffice.org Calc с данными блокнота и диаграммой (53,9 кб).