Вычисление параметров для построения многоугольников Пуансо

Разделим окружность, имеющую радиус R, с помощью циркуля на n равных частей и соединим точки деления хордами длиной l (l - раствор циркуля, с которым производится деление). Если точки деления соединить последовательно, то получится выпуклый многоугольник. Если точки соединить через одну, две и более точек, то получатся звездчатые многоугольники. Например, при n = 5 получаются два пятиугольника: выпуклый и звездчатый.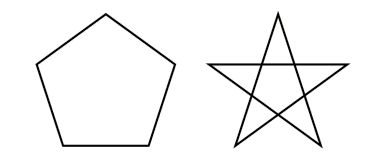

Изучением таких многоугольников занимался французский математик и механик Луи Пуансо. Он называл их настоящими, а число их N для заданного n определял по формуле:

N=n/2*(1-1/a)*(1-1/b)*(1-1/c)*...,

где a, b, c, - различные (не равные 1) простые множители числа; n ≥ 3.

Для заданных значений R и n ≥ 3 программа вычисляет величины l и N для построения многоугольников Пуансо.

Исходные данные заносятся в ячейки памяти: n → П7, R → П8.

Результаты вычислений записываются в ячейки памяти: N → П4, l → П9.

Инструкция по пользованию программой для МК-52 с БРП-4

• 1. Наберите адрес 1354277 и введите программу, нажав клавиши А↑, ↑↓.
• 2. Установите переключатель Р/ГРД/Г в положение Р.
• 3. Введите исходные данные.
• 4. Включите счет, нажав клавиши В/0, С/П. Время вычисления зависит от значения n.
• 5. Считайте результаты.
• 6. Для повторного запуска программы повторите пп.3-5.

Инструкция по пользованию программой для ЭКВМ

• 1. Загрузите программу с нулевого адреса.
• 2. Клавишей Р-ГРД-Г установите размерность "Р" - радианы.
• 3. Введите исходные данные.
• 4. Включите счет, нажав клавиши В/0, С/П.
• 5. Считайте результаты.
• 6. Для повторного запуска программы повторите пп.3-5.

Тестовый пример

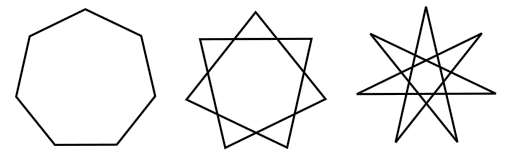
Программа "Вычисление параметров для построения многоугольников Пуансо"

Программа 52 из блока расширения памяти БРП-4, переключатель "1/2" блока в положении "2", адрес 1354277.

Файл brp4-52.mkp (КС 9909/139)

Исходный текст для кросс-компилятора

Файл brp4-52.mkl

.CHARSET 1251

;БРП-4
; 52. Вычисление параметров для построения многоугольников Пуансо (2 - 1354277)

.ORG 0
	F PI
	RM 7
	/
	F SIN
	RM 8
	*
	2
	*
	M 9
	1
	M 3
	RM 7
	2
	/
	M 4
	K FRAC
	F X=0 A33

A18:	 ; с адреса 23
	F ANS
	M 7
	2
	/
	K FRAC
	F X!=0 A18
	1
	ENT
	2

A28:	 ; с адреса 59
	F 1/X
	-
	RM 4
	*
	M 4

A33:	 ; с адреса 16
	RM 7
	F SQRT
	M 6

A36:	 ; с адреса 48
	RM 6
	RM 3
	2
	+
	M 3
	-
	F X>=0 A61
	RM 7
	RM 3
	/
	K FRAC
	F X=0 A36

A50:	 ; с адреса 55
	F ANS
	M 7
	RM 3
	/
	K FRAC
	F X!=0 A50
	1
	RM 3
	GOTO A28

A61:    ; с адреса 42
	1
	RM 7
	F 1/X
	-
	F X!=0 A70
	RM 4
	*
	M 4

A70:	 ; с адреса 65
	RM 4
	9
	F 1/X
	+
	K INT
	M 4
	R/S
.END 

Примечание.

Пуансо (Poinsot) Луи (3.1.1777, Париж, — 5.12.1859, там же), французский математик и механик, член Парижской АН с 1813. Окончил Политехническую школу в Париже (1797), с 1809 профессор там же. В период Июльской монархии — в Министерстве народного образования. Пэр Франции (1846), сенатор (1852). Первые работы П. посвящены теории правильных звездчатых многогранников. В 1803 опубликовал "Элементы статики", в которых применил разработанные им геометрические методы исследования к учению о равновесии твёрдых тел и их систем. В 1834 построил теорию вращения твёрдого тела вокруг неподвижной точки. Впервые ввёл понятие эллипсоида вращения.

(Статья из БСЭ)